Aklın Çalışma Hızını Gösteren Dada Yayları: Yeni Bir Teorem

‘’Gerçeğe giden her yol, basit ama derin bir sorguyla başlar. Akla düşen her sorunun cevabını Tanrı kainatta gizlemiştir. Cevabı sadece hesap bilenler bulur. Çünkü, Tanrı kainatı hesap ile yaratmıştır.’’

(Esma-Hazik Aydın)

Johann Bernoulli henüz 30 yaşının eşiğindeyken zihnine bir soru takılır. Soru: ‘’Yüksek bir kulede bulunan kişinin, en kısa sürede yere inebilmesi için nasıl bir kaydırak kullanmalıdır’’? şeklindedir. Ve bunu önemli bir dergide ödüllü bir soru olarak yayınlar. Bernoulli yaptığı uzun ve dahiyane hesaplar sonunda en hızlı kaydırağın sikloid eğrisi şeklinde olması gerektiğini bulmuştur. Galileo’da daha önce bu problemi kendine sormuş: ’’Çembere yakın bir yay olmalı.’’! şeklinde bir cevap bulmuştur. Nitekim, Bernouli’den yıllar önce Galileo bu eğriyi en kapsamlı incelemiş ve ona SiKLOiD adını vermiştir. Sikloid üzerine kalıcı çalışmalar yapan bir diğer kişi Blaise Pascal’dır. Peki sikloid nedir?

Bir çemberin üzerine sabit bir nokta işaretler ve onu  düz bir masa üzerinde yuvarlarsanız bu noktanın dikey düzlemde takip ettiği yol sikloid eğrisi olur.

Bernouli’nin son derece kıskanç ve takdir hissinden uzak biri olduğuna dair çok ilginç bir hikaye vardır. Oğlunu bile kendi kazanmak istediği bir matematik yarışmasına katıldığı için evden kovmuştur.  Johann Bernoulli sorduğu soruya gönderilen cevaplar arasından birinde sorunun doğru cevabının verildiğini bulur. “Aslan pençesinden belli olur” der. Nitekim çözümün altına: “Isaac Newton” yazmaktadır.

Christiaan Huygens’te 1659’da sikloid eğrisiyle ilgili bir başka ilginç problem ortaya atmıştır. Bir çanağın kenarından bir bilye bırakır ve çanağın içinde yuvarlanışını izlersek, her yuvarlanışta bilyenin eriştiği yüksekliğin azaldığını ve her salınımının süresinin de birbirinden farklı olduğunu görürüz.

Soru şöyle idi: Çanağın şekli ne olmalı ki bilye yavaşlasa bile her salınımının süresi aynı olsun? Bu probleme Tautochrone Problemi, yani Eş Zaman Problemi denir. Huygens bu problemi çözmüş ve çözümün bir sikloid eğrisi olacağını göstermiştir.

Köyde bir gün, karmaşıklığın ve zihinden hesabın ustası olan annem Esma; ve, sadelikle sanatın ustası olan babam Hazik Aydın’la şöyle bir ustalık konusu tartıştık: ‘’Dağın tepesinde olan yayladan aşağı eşya inişini sağlamak ve işleri kolaylaştırmak için nasıl bir kaydırak tasarlabnabilir’’? İkisi de soruya değişik ama buradakine yakın cevaplar vermişti. Ben ise, sorunun cevabını burada anlatıldığı gibi kitabi olarak vermiştim. Onların bu cevap tarzıma olan isyancı ve alaycı bakışları hafızamdan asla silinmedi. Kardeşim, eşim ve çocuklarımız da değişik matematiksel epirilerle yeni ilham kaynakları olmuşlardı.

Annem ve babam adeta aynı anda düşünmüşlercesine bana şu soruyu sordular: Neden bazı insanlar hızlı düşünürken bazıları yavaş düşünür? Bunun da bir metodu varmıdır.?.

Soruya verdiğim cevaplar tatminkar değildi. Tüm tahsil hayatımla birlikte  adeta hiçliğe itilmiştim. Babam bana dedi ki: ‘’Soruya anlamadığımız şekilde cevap verdin. Sen bu konuyu bilmiyorsun. Hiç kırlardan taş yuvarlamadın mı? Kırların yüzey şekilleri ile taşın hızı farklılık arzeder. Keşke aklını mühendislikte kullansaydın, daha iyi olurdun’’.  Annem ise, evin önündeki danayı ve kediyi işaret ederek: ‘’Bak, kedi neden danadan da pratiktir, düşün….!’’ dedi.

Yıllarca düşündüm. Ve cevabı bu yılın başında buldum. Bu özet Türkçe cevabımı  size yazıyorum. İngilizcesini de bir dergiye gönderdim.

Laboratuvarda bir gece yarısı ratlara ait beyin resimleri çekerken ekrana paryetal loblar düştü. Paryetal kortexlerin dış yaylarının şekillerini ve trigonometrik denklemlerini  düşündüm. Bir an aklıma annem ve babamın sorduğu soru da yıldırım gibi hafıza alanlarına düştü. Çakan bu şimşeğin ışığıyla, SİKLOİD eğrisi ve denklemleri  uzaktan gözüme iliştiler. Evet, kedinin beyin kabuğu dananın beynininkine göre sikloid eğrisine daha yakındı. Genellikle hastalarımı dijital kayda alırım. Hemen hızlı düşündüğünü bildiğim esprili hastalarımın beyin görüntülerini aramaya başladım. Yaklaşık 100 hastamın görüntüsünü inceledim. Evet: Hızlı düşünenler, yani beyinlerinin RAM gücü fazla olanlarda temporoparyetal kortexin ve iki beyin yarıküresini birbirine bağlayan korpus kallozumun şekli sikloid eğrisine daha yakındı. Denklemleri de yaklaşık sikloid eğrisinin denklemine eşit olmasa da denkti.

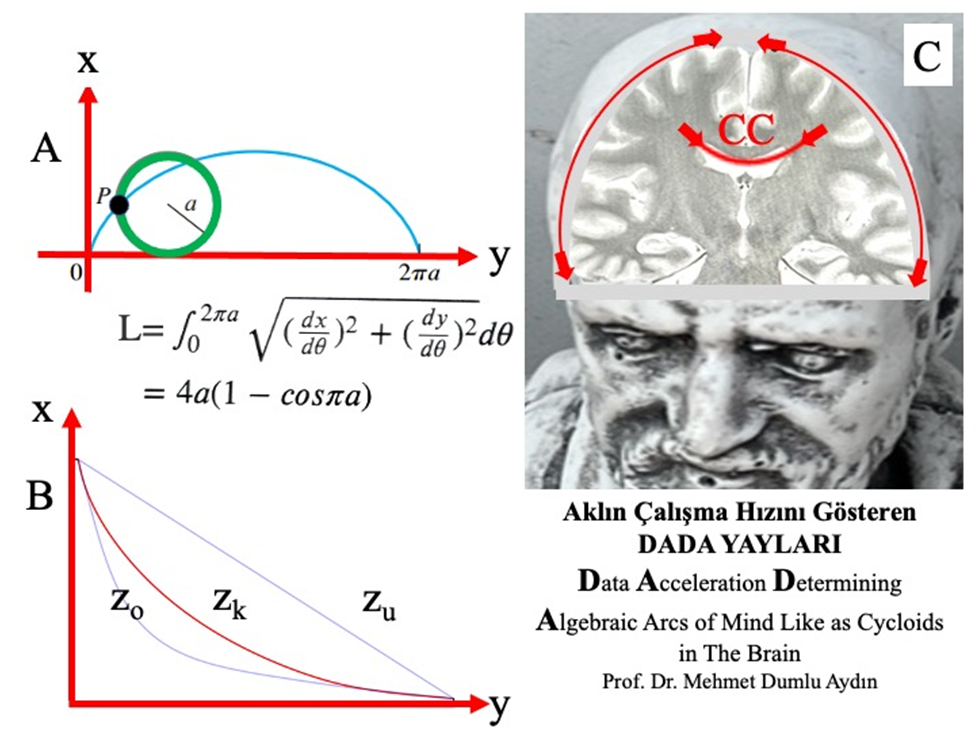
Yukarıdaki şekil A’da, üzerinde siyah bir nokta konulmuş yeşil çemberin yuvarlanmasıyla oluşan Sikloid Eğrisi görülmektedir. Bu eğrinin trigonometrik parametrik denkleminin integrali alınırsa boyu (L) da kolayca hesaplanabilir. Şekil B’de, X konumundan Y konumuna inmek için çeşitli yollar verilmiştir. İlk planda, Pisagor teoremine göre, hipotenüs olan Zu’nun en kısa yol olduğu kesindir. Oysa burada mekanın değil zamanın yasaları geçerlidir. Dolayısı ile, en kısa zamanlı yol ortada olan sikloid şeklindeki Zk (kısa zaman) yolu;  soldaki sikloidimsi eğri orta zamanlı yol Zo (Z orta zaman) yolu. Ve en uzun zamana mal olan da hipotenüsü temsil eden ve mekânsal olarak en kısa olan yol olan Zu ( uzun zaman) yoludur (Resimler kendi çizimlerimdir. Ya da kendi arşivime aittir. Bilimsel kanıtlar ve denklemler kaynaklardan alıntıdır).

Aynı yasaları beyne uyguladığımızda, beynin düşünme ve karar alma mekanizmalarında esas beyin parçaları olan paryetotemporal kortexin ve iki beyin yarıküresini birbirine bağlayan korpus kallozumunun (CC) yaylarının da sikloid olduğu gerçeği ile karşılaşırız.

Ben, kendi tasarımım olan metodla, beynin ve dolayısı ile aklın çalışma hızını somutlaştırabilmek için, sikloid eğrileriyle düşünce hızını  belirleyen beyin kabuğu, korpus kallozum ve hipokampal yüzeylerin eğriliklerinin birbirine denk olduğunu müşahade ettim. Bu bilgiler resim C’de verilmiştir.  Ve bu yaylara, İngilizce yazdığım makalenin başlığında büyük oranda tesadüfi olarak gizlenen ilk dört kelimenin ilk harflerini alarak, literatürde de kolay adlansın diye DADA ARCS (DADA YAYLARI) ismini koydum.

Makalenin İngilizce başlığı aşağıdaki gibidir:

Data Acceleration Determining Algebraic Arcs of Mind Like as Cycloid in The Brain: A New Thorem

Cevabı bulmuştum. Ama anneme ve babama müjde veremedim. Ekmeklerini tırpan, tırmık, yaba, dirgen orak, çekiç …. ve örsle  topraktan çıkaran bu iki natürel filozof, atomlarını  ve bilgilerini ödünç aldıkları evrene iade için SONSUZİSTAN’a göçmüşlerdi.

Makaleden Alınacak Dersler:

1. Matematik ve fizik yasaları birbirinden bağımsız olsa gerektir. İrrasyonel ve karmaşık sayılar anlaşılmadan, yeni sayı sistemleri keşfedilmeden hakikat anlaşılmaz (Şekil A). Bu acak güçlü beyinler gerektirir (Şekil C).
2. Zaman ve mekan yasaları birbirinden bağımsızdır (Şekil B).
3. Matematik ve fizik bilgisi olmadan hakikat anlaşılamaz.
4. Her bunalım, içinde sonsuz diriliş denklemi bulunan bir tohumdur. Bu tohumlar, sadece büyük düşünen büyük beyinlerde zafer çiçekleri açar.
5. Dehayı ızdırap doğurur.
6. Eğitim ve öğretim, uyandırıcı ve aydınlatıcı değilse dehayı köreltir.

Kaynaklar:

1. Prof. Dr. Ali Sinan Sertöz  Bilkent Üniversitesi – Fen Fakültesi – Matematik Bölümü BilimveTeknik Mart 2017
2. Cajori, Florian (1999). A History of Mathematics. New York: Chelsea. p. 177. ISBN 978-0-8218-2102-2.
3. Tannery, Paul (1883), “Pour l’histoire des lignes et surfaces courbes dans l’antiquité”, Bulletin des sciences mathèmatique, Paris: 284 (cited in Whitman 1943).
4. Wallis, D. (1695). “An Extract of a Letter from Dr. Wallis, of May 4. 1697, Concerning the Cycloeid Known to Cardinal Cusanus, about the Year 1450; and to Carolus Bovillus about the Year 1500”. Philosophical Transactions of the Royal Society of London. 19 (215–235): 561–566. doi:10.1098/rstl.1695.0098. (Cited in Günther, p. 5)

Bu yazı; aynı zamanda bana bir harf ve düşünmeyi öğreten tüm öğretmenlerime; beyin cerrahiyi bana öğreten hocalarıma; özellikle de matematik öğretmenlerim olan İsmail Alay, Yalçın Özmen, Saffet Kaya, Zafer Sancar ve Osman Pala hocalarıma ithaf edilmiştir. Onlar olmasa idi bu makale olmazdı.