Karlı bir İstanbul gününden merhaba. Kar yağınca duyulan sevincin sebeplerinden biri sanırım çocukluk çağındaki anılarımız. Arkadaşlarla yapılan kar savaşları… En önemli anı da okulların tatil olması elbette. Günlük koşuşturma içinde işlerimizin aksaması, trafiğin tıkanması, yolda yürürken düşmek vb. problemler olsa da kar yağdığı zaman sevinmeyen yoktur sanırım.
Kar tanesi… Her bir kar tanesi eşsizdir. Biri diğerine benzemez. Şekilleri ise tıpkı doğadaki diğer mükemmel eserler gibi farklıdır, fraktaldır.
Atomdan kâinata kadar her şey belli bir matematik ölçüsünde tasarlanmıştır. Bu tasarım; kimi zaman yaygın olarak kullanılan matematik ve fizik formülleri ile açıklanırken bazen de hali hazırdaki bilgi ve tecrübe, bu durumu tanımlamaya yetmez. Doğanın modellenmesi gibi. Bu modellenme nasıl eğriler, çizgiler, üçgenler ve diğer geometrik şekiller ile açıklanabilir? Öklid geometrisi ile bu modellenmelerin yapılamacağının anlaşılmasından sonra dikkatler Benoit Mandelbrot tarafından önerilen fraktallara çevrildi. Latince fraktus (kırık) olarak isimlendirilen bu yapılar; büyükten küçüğe, küçükten büyüğe birbirine benzeyen birçok geometrik şeklin oluşturduğu, sonsuzluğa doğru giden, kompleks ve göz kamaştırıcı şekillerdir.
Fraktalların temelinde bir ana şekil vardır ve bu şekil sonsuza kadar kendini tekrar ederek bütünü oluşturur. Ağaçlar, eğrelti otları, brokoli, karnabahar, şimşek, elektrik, coğrafi arazi ve nehir sistemleri, bulutlar, kristaller ve çok daha fazlası doğada görülen fraktallara örnek olarak verilebilir. Canlılardaki dolaşım ve solunum sistemi de fraktaldır. Bu örneklerin yakından incelenmesi ile her bir parçanın bütünün bir kopyası olduğu kolaylıkla görülebilir.

Güzellik ve estetikten bahsederken altın orandan (Fi yani φ) da söz etmeliyiz. Altın oran, her sayının kendinden öncekiyle toplanması sonucu oluşan bir sayı dizisi olan Fibonacci Sayıları olarak da bilinmektedir. Bir Fibonacci sayısının kendinden önceki sayıya bölümü ile elde edilen sonuç, 1.618’dir, yani altın orandır. Estetik güzellik ölçüsü olarak nitelendirilen altın oran; spiral galaksilerde, insan vücudunda, bitkilerde, hayvanlarda kısacası en büyük mimarın eserlerinde kolaylıkla gözlenebilir. Bununla birlikte Mimar Sinan ve Leonardo Da Vinci gibi birçok sanatçı da eserlerini üretirken altın oranı kullanmıştır.

Üreme dinamiklerinde de altın oran söz konusudur. Arı fizyolojisi, altın orana verilecek en güzel örneklerdendir. Arı kolonilerinde dişi arı sayısı erkek arı sayısına bölündüğünde altın oran elde edilmektedir. Erkek arıların tek bir ebeveyni (dişi arı) ve dişi arıların iki ebeveyni (bir dişi ve bir erkek) vardır. Aile ağacı çizildiğinde erkeklerin 2, 3, 5 ve 8 olmak üzere büyük, büyükbüyük, büyükbüyükbüyük ve büyükbüyükbüyükbüyük ebeveynleri (gr-gr-gr-grandparents) olduğu görülür. Bu durum dişilerde ise 2, 3, 5, 8, 13 şeklinde devam eder. Hayvanların saldırı modelleri de benzer şekildedir. Bir şahin avına yaklaştığında, en keskin görüşü onun uçuş yönüne göre bir açıdır ve bu açı da altın orandaki spiral eğim ile aynıdır.
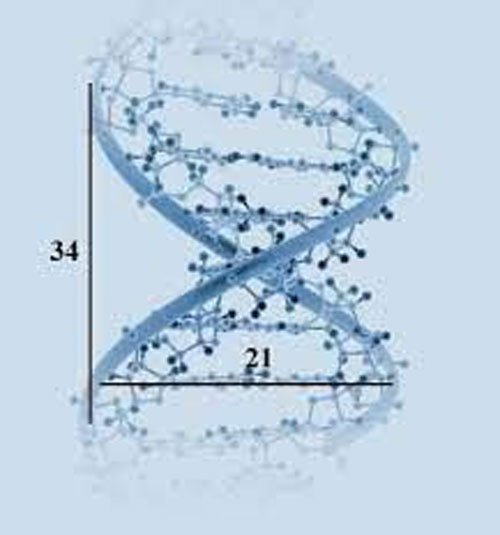
Tabi ki DNA… Kalıtım molekülümüz, bütün özellikleri belirleyen çift iplikli sarmal yapı. Hücre dışına çıkarıldığında yaklaşık 2 metre uzunluğundaki bu molekül, nükleozomlar aracılığıyla kat kat kısalır ve nükleus içine sığar. Uzunluğu 34 Angström ve genişliği ise 21 Angström’dür (1 angström; santimetrenin yüz milyonda biridir). Bu iki sayı, art arda gelen iki Fibonacci sayısıdır ve oranı 1.6190476 yani yaklaşık altın orandır.
Galileo Galilei, “Evrenin dili, matematiğin diliyle yazılmıştır. Bu dilin harfleri üçgenler, çemberler ve öteki geometrik biçimlerdir” demiştir. Matematik kurallar çerçevesine hareket eden doğa, kendi içinde birbirinin işine karışmayan olaylar dizisi üretmekte ve birbirinin işine müdahale etmeyen canlıları barındırmaktadır. Farklı düşüncelere ve bu düşünceler neticesinde ortaya çıkan hareketlere saygı göstermek. Huzuru, mutluluğu ve başarıyı da getiren bu tutum değil mi zaten?
