Ekmeğin Destanı

183

«Bir adam vardı. Suyu arıyordu. Toprağı üç kulaç, beş kulaç kazdı. Suyu bulamadı. On kulaç, on beş kulaç kazdı. Gene suyu bulamadı.  Sonra yerin derinliklerinde kara kaya tabakalarına rastladı. Yeis’e düştü, gücü sona erdi ve Suyu bulmaktan ümidini kesti. «Fakat bir ses ona: — Daha derinlere in, daha derinlere! dedi. Daha derinlere indi ve suyu buldu.»
Suyu Arayan Adam/Rama Krişna/ŞSA

İlk deneysel hatıram, tahıl ambarımızda ekmeklik olarak sakladığımız buğdayların bir bahar mevsiminde büyük bilge amcam tarafından çuvallara doldurularak tarlada toprağın karanlığına gömülmek üzere götürülürken döktüğüm gözyaşlarıyla yeşermiştir ve hala yeşildir. Amcam, ertesi sabah beni güneşle uyandırdı. Eski evde bulunan ambara gittik.

 Bana çuvalın ağzını tutturdu, kendisi de buğdayları çuvallara doldurdu. Sonra kağnıya yükledi. Tarlanın yolunu tuttuk. Amcam iki gün boyunca tarlayı sabanla sürdü, sonra tapanla düzledi. İki gün daha tarlayı yeniden sürdü. Beline bağladığı peştamala doldurduğu buğdayları tarlaya serpti. Ve tekrar tapanladı. Amcamın serptiği buğdayları kuşlar kaçırırken öküzler de var gücüyle onları toprağa gömüyordu. Ben ise buğdayların mezara girişine ve bu nedenle de hasret kalacağımız buğday ekmelerine olan özlemimle ağlıyordum.

Amcam bana cebinden birkaç şeker uzatarak gönlümü almak istediyse de olmadı. Bana döndü ve: ‘’ Bak yeğenim, bu buğdayları yeşersin, büyüsün, yeni buğdaylara dönüşsün ve ekmek olsun diye toprağa ektik. Onlar yeşerip daha fazla buğday verecek, daha fazla buğdayımız olacak. Toprağa ekilen tohum yeşerir,   dirili ve hayat bulur, bunu unutma! dedi.

Çok ağır geçen bir kış mevsiminde ambarda un tükenmiş, değirmenin nemlenen ambarı, taşları, buz bağlayan çarkları nedeniyle buğdaylardan kaliteli un yapmak o an için mümkün olmamıştı. Gelen güzel baharda annemin: ‘Artık bahar erişti. Ekmek üretme zamanımız geldi’’ deyişi bir müjdeydi …

 Bu benim hayata karşı ilk uyanışımdır. Sonra tarla yeniden tapanlandı ve eve döndük. Annem de evdeki çavdar ve arpaları yıkadı, kuruttuk, öğüttük, un ve ekmek yaptık. Harikaydılar Amcam zaman zaman beni o tarlaya götürür, adeta yaptığı deneyin sonuçlarını gösterirdi. Sonuçlar mükemmeldi. Tarla yemyeşil, sonra gri, sonra gök, sonra buğdaylarla beraber buğday rengi ve çuvallarca buğday oldu ….  Sevinçten dört değil sonsuz köşeyiz. Ve orakla biçin, harman, buğdayların yıkanışı, kurutuluşu, öğütülüşü, un oluşu, yoğruluşu, tandıra girişi ve ekmeklere dönüş… artık ağlamayacaktım. Annem de buğday ekmeklerimiz var diye kimseden utanmayacaktı ….. Dr. Fethi Bey’in Değirmen Taşları için yazdığı bir yazı vardır. Derki;

‘’Un yapayım diye dönen iki taş,

Duran bir kafaya denk tutulur mu?

Acaba yıllarca düşünse insan,

Bu iki taştaki sırrı bulur mu?

O halde, kendine sunulan buğday adlı bilgiyi un adlı bilgiye çeviren iki değirmen taşı kadar faaliyete sahip olamayan iki beyin yarımküresine sahip olmaktan utanmalıyız. Ben bu kez ambardaki buğdayları merak etmeğe başlamıştım. Çünkü onların rahattı. Toprağa ekilip çile çekecek bir yola girmemişlerdi. Ve amcamla ambara gittik. Evet ambardaki buğdaylar yeşermemişti….  Bu benim riski ilk fark edişimdir, uyanışımdır. Yandaki şekilde, annem ve babamın 70’li yaşlardaki halleri izlenmektedir. Bu insanlar ekmeklerini topraktan çıkardıkları için ebedi kurtuluşa erdiler ……. 

Harman Makinesi İle Saman ve Buğdayların Ayrılışı

Harman makinesinin genellikle sağ tarafında yerleşik ve elle çevrilen büyük bir S kolu büyük olan dişliye bağlanır ve o da daha küçük bir dişliye bağlı pervane sistemini çevirerek samanı ekinden ayıran rüzgarı yaratırdı.

Yanlarda bu dişli çark ile bir boksörün kollarının hareketini andıran mekanik bir sistemle elekler sallanır ve saman-taş-ekin birbirinden ayrıştırılırdı. Burada kol hızlı çevrilirse taneler samana ve yavaş çevrilirse saman ekine karışırdı. Bunun için de belli bir limitte kolun bükülmesi gerekirdi. Samandaki taşlar da bu düzenekte en alttaki eleğin altına akardı. Harman makinelerindeki  büyük dişlinin küçük dişlinin çapına oranı da e sayısına yakın bulunmuştur. Harman makinesinin kolunu hızlı çevirirseniz ekin samana gider, yavaş çevirirseniz saman ekine karışır. O zaman bunun ideal çevirme hızı nedir?

Şu buğdaylardan birkaç çuval yıkayıp kurutarak un yapalım, ekmek pişirecek un kalmadı’. Deyişi üzerine amcamın: ‘Onlar tohumluk olsun, çavdar ve arpamız daha çok var, onları yıkayın ve kurutun. Onlardan un çıkaralım.’ Şeklindeki kararı ile yıkılmıştım. Çünkü şehirden gelen medeni insanlara arpa ve çavdar ekmeği ikram etmek ayıptı. Buna annem de çok üzülmüştü.

Saban, kağnı ve değirmen …  insanlığın en büyük üç icadı … Her üçünde de keşfedilmiş ve keşfedilecek tüm fizik ve matematik yasaları mevcut. Değirmende işleyen yasaları çok sade bir mantıkla özetleyelim: Değirmende taneciklerin öğütülmesi için enerji kaynağına, öğütücüye , taneciklerin öğütücüye ritmik olarak dökülmesi için bir dökücüye ve toplayıcı bir ambara gerek vardır.

Enerji kaynağı olarak köyümüzdeki değirmenlerde su kullanılırdı. Bu su bir oluktan akan su, değirmenin adeta bodrum katına yerleştirilmiş 24 pervane levhası olan yatay bir çarkı çevirir. Bu çarkın merkezine bağlı bir mil, bodrum kat üstünde olan silindir şekilli sabit bir taşın üstünde aynı çaptaki bir başka taşı döndürür. Taşın ortasında oyulmuş bulunan silindirik bir boşluğa ekin ambarından saniyede 3-8 adet miktarında belli bir hız ve aralılarla dökülen tanecikler bu taşlar vasıtasıyla un haline getirilir ve dönen taş tarafından un ambarına aktarılır.

Şimdi Değirmendeki Fizik ve Matematik Yasalarını Ele Alalım:

Suyun değirmen oluğundan ideal olan en hızlı  şekilde akması ve çarkı en ideal hızda döndürmesi için oluğun silindirik olması ve yere 45⁰lik açı ile konumlandırılması,  suyun en ideal hızda oluktan çıkması için  oluktan çıkış yerindeki çapının, suyun oluğa giriş açıklığının çapından daha dar olması gerekir. Ayrıca yatay konumdaki çarka da suyun yatay vurması gerekir. Oluğun alt kısmı olan şüşürt denilen kısmından çıkan suyun eliptik kesiti içine düşen çarkın pervane kanat sayısı en az 45⁰’lik açıyı sürmeli vi dişli sayısı da bu elipsin ¼’üne tekabül etmelidir. Dişli sayısı çok olursa çark yüzeyi bir düzleme yaklaşacağı için su çark üzerinden kayar ve çark yavaş döner. Pervane levha sayısı az oluşa suyun enerjisi bölünür ve çark yine yavaş döner. Biz incelediğimiz değirmende çarkın pervane levha sayısını 24 olarak bulduk.

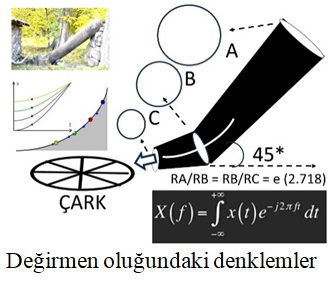
İki dik kenarının uç noktaları arasındaki en kısa geometrik yol hipotenüs olmasına rağmen, dikey konumda iken düşen cisimlerin en kısa sürede akmaları için bunun bir brakistokron eğrisine benzemesi gerekir. Değirmen oluğunda giriş çapı, şüşürt çapı ve suyun çıkış alan çapları arasındaki oran yaklaşık 2.718 yani e sayısına eşittir. Oluğun içinde suyun akış eğrisi brakiostokron eğrisine yakındır. Yukarıdaki resimde soldaki eğriler bunu göstermektedir.

Değirmen taşı hızlı dönerse taşlar ısınır ve un yanar. Yavaş dönerse un kalın olur. Tanecikler fazla akarsa un kalın olur, az akarsa un yanar. Çakçak hızlı vurursa ekinler taşın yüzeyine dökülür, yavaş vuruşa ekin az akar.  Değirmen yeni öğütmeye başladığında taşın civarına yol kenarlarına biriken kar gibi un birikir. Ve bu yöre unun civara taşmasını engelleyerek ambara akıtır.  Sonra oradan çuvallara un doldurulur ve ağaçtan silindir sütunla da un bastırırlar ve evdeki ambara götürülür boşaltılırdı.

Değirmenin çarkı dolayısı ile taşı hızlı dönerse buğday-arpa-mısır … tanecikleri çok fazla parçalanır, taş ısınır ve un yanar. Yavaş dönerse taneciklerden iyi un oluşmaz ve köy tabiriyle un ince olur. Taş ışık hızıyla dönerse ne olur? Taşın yüzey alanı, ambardan akın ekinin debisi, çarkın dişlerinin sayısı ve boyu, değirmen oluğunun yere göre 45 derecelik konumu, oluğun suyun girdiği ve çıktığı giriş ve çıkış ağızlarının aşan oranı ne olmalı ki su en hızlı çarpsın? O zaman taşın ideal dönme hızı nedir?

Değirmen Oluğundan Akan Suyun Esrarı?

Özel görelilik kuramında mevcut bilimsel düşünceye aykırı olsa da deneylerle deneylerle ispatlanmış postulatları vardır. Bu postulatlardan; kütle-enerji eşitliği (E=mc²), hareket eden cisimlerin  kısalması ve zamanın genişlemesi olayı önemlidir. Bu teorilere göre hareket halindeki saatler daha yavaş işler. Boyun kısalmasını ve zamanın genişlemesini ifade eden γ katsayısı Lorentz Faktörü olarak bilinir ve      γ = (1 − v²/c²)^−1/2 ile ifade edilir. Bu denklemde v nesnenin hızı, c’de ışık hızıdır. γ ile 1 arasındaki fark ışıktan çok daha düşük olan hızlar için göz ardı edilebilir. Yani özel göreliliğin Galilean göreliliğine yaklaşıldığı bir durumda hız göreceli olarak yükselir ve cismin hızı ışık hızına yaklaştıkça eğri sonsuzluğa doğru sapar. İşte bu nedenlerle şüşürt kısmında hızı artan su beyaz gözükür.

Buğday Tarlalarında; Göklerdeki Bayrağımızın Hilalinin Nuru Altında Onun Yerdeki Temsilcisi Olan Tırpan ve Orağın Parlayan Hilalleriyle  Ekmek Üreten  Ellerin  Duası

Tırpan, orak, yaba …dirgen, tırmıkla…
Ekmeğin ham maddesini üreten buğday tarlalarında…
En kutlu duanın en kutlusu yapılmış ….
Dikenlerle süslenen  öpülesi elleri …
Öpmek için yere inmiş melekler ….
Bu nasırlı ellere tüm melekler ağlamış ….
Kabul olmuş buğdaylı ellerin dilekleri …Allah katında …
Dünyada açlıktan ağlayan bebek kalmamış!
Bomboş parlayan ellere …..bile, buğday yetiştirsin diye ….
Denizler buharlaşmış bulutlara su vermiş…Dağlara kar göndermiş…
Karlar aşkından erimiş, ırmaklarla tarlalara akmış …
Bulutlar başaklar büyüsün diye tarlalara göz yaşı dökmüş
Toprağa azot geçsin diye şimşek çakmak için gökler parçalanmış …
Ulu Tanrı; bu ellerin dualarını kabul ederken …
Hak etmediği ekmeği yiyenlerin duası asla Arşa ulaşmamış …
Böyle ameller ile mutlu olunur; huzura erişir cihan ….
Saban, tırpan, orak, yaba, dirgen ve tırmıktaki esrarı anlarsa insan …
İşleyen demir ışıldar; işleyen beyinde parlar akıl, vicdan ….
Amel defterlerine ancak patlayan ellerle yazılır kat, kat iman ….
Doldurmaz ambarı, kalbi, beyni …. tembellerin efsanesi….
Uzaklaşır hak katından cümlesi, sayıların çarpımı kadar ışık senesi …
Dada